Treść problemu: Jeśli rozwiązanie problemu jest łatwe do sprawdzenia pod kątem poprawności, to czy problem musi być łatwy do rozwiązania?

Definicje

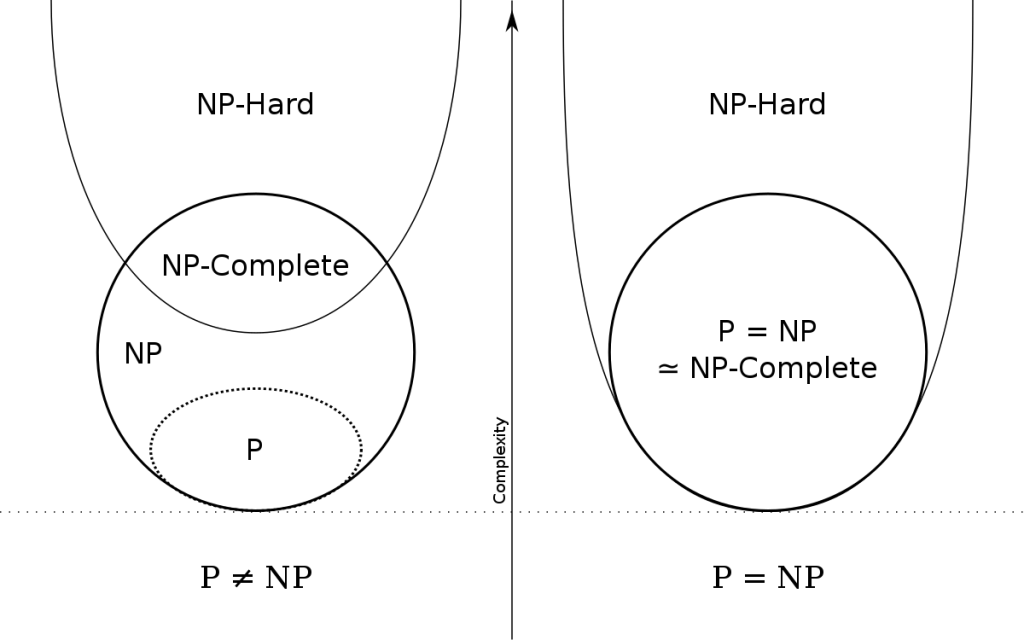
Problem decyzyjny – pytanie, którego możliwymi odpowiedziami są tylko tak i nie.

Problem P (ang. deterministic polynomial, deterministycznie wielomianowy) – problem decyzyjny, dla którego rozwiązanie można znaleźć w czasie wielomianowym.

Problem NP (ang. nondeterministic polynomial, niedeterministycznie wielomianowy) – problem decyzyjny, dla którego rozwiązanie można zweryfikować w czasie wielomianowym.

Wykonanie czegoś w czasie wielomianowym oznacza, że czas potrzebny do otrzymania wyniku jest funkcją wielomianową wielkości problemu, czyli O(n^x).

Na czym to polega?

Dla lepszego zrozumienia tej kwestii warto posłużyć się przykładami.

Problemem P jest np. sprawdzenie czy wszystko co mamy na liście zakupów, znajduje się w naszym koszyku. Do otrzymania rozwiązania musimy dla każdego z n-produktów na liście sprawdzić n-produktów w koszyku, co oznacza, że złożoność czasowa tego problemu to O(n^2), czyli funkcja wielomianowa.

Natomiast problemem NP jest np. zweryfikowanie poprawności podanego kodu do odblokowania zamka. Możemy to zrobić bardzo szybko po prostu go wpisując. Jednak żeby znaleźć rozwiązanie dla tego problemu (poprawny kod) potrzebujemy dużo więcej czasu, jego złożoność czasowa będzie wynosić O(10^n), czyli funkcję wykładniczą jego wielkości.

Dlaczego P vs. NP?

Upraszczając maksymalnie tę kwestię, problemy klasy P są NP, ponieważ można je łatwo sprawdzić. Nie wiadomo natomiast czy istnieje problem NP, który nie jest w klasie P (czyli czy P różni się od NP). Innymi słowy, czy istnieje problem, który z całkowitą pewnością można rozwiązać wyłącznie w czasie wykładniczym. Jest to jeden z problemów milenijnych i za jego rozwiązanie przewidziana jest nagroda w wysokości miliona dolarów amerykańskich.

Czemu to takie ważne?

Jeśli P = NP, to nasz świat musiałby się zupełnie zmienić. Systemy kryptograficzne oparte na rozkładzie liczb na czynniki pierwsze (problem NP) przestałyby być bezpieczne, ponieważ można byłoby je bardzo łatwo złamać. Spowodowałoby to upadek serwisów internetowych, sektora finansowego czy administracji publicznej.

Przewidywania

Pomimo, że nie ma pełnego dowodu na żadną z możliwości rozwiązań problemu P vs. NP., to przewiduje się, że wkrótce pojawi się on dla tezy, że P ≠ NP. W 2000 roku Samuel Buss przewidywał, że P ≠ NP zostanie potwierdzone w ciągu 20 lat. Według New Scientist z 2010 roku istnieje 50% szans na rozwiązanie problemu przed 2024 rokiem. W 2012 roku analiza 144 hipotez matematycznych (w tym tych nieudowodnionych) uwzględniająca wzrost liczby matematyków oraz coraz lepszy przepływ wiedzy pomiędzy nimi wykazała, że szansa na rozwiązanie problemu P = NP. przed 2024 rokiem to 41%.